/02/21 · こんにちは。相城です。今回は球の表面積について書いていこうと思います。 中学生でも納得かな?なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 · r r の球の表面積は S=4\pi r^2,\ S = 4πr2, 球の体積は V=\dfrac {4} {3}\pi r^3 V = 34 πr3 である。球の体積の考え方の例 -πr³ 球の表面積の考え方の例 4πr² 4 3 円がぴったり 入る円柱 円がぴったり 入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める

球の求め方教えてください Clear
球 表面積 求め方
球 表面積 求め方- · 円のように見えないこともないので,この図形を円と捉えることにする. 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1 · よって,球帯の表面積は S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ S=2\pi r^2\int_{\theta_1}^{\theta_2}\cos\theta d\theta S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ (ただし, θ 1 \theta_1 θ 1 は球帯の底面の緯度, θ 2 \theta_2 θ 2 は球帯の天面の緯度)



Search Q E5 86 86 81 Ae E9 9d E7 8d Tbm Isch
· 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための語呂は、 · 面積分での球の表面積の求め方を教えてください。 球座標系(r,Θ,φ)の2変数の面積分により、半径aの球の表面積を導出せよ。 おしえてください。お願いします。ゾウの表面積を求める公式は以下の通りです。 ゾウの表面積の求め方 45 ( 6807 × 身長 ) ( 7073 × 前足の太さ ) なんでこんな式になるんでしょうか? 特に最初の45は一体何なのか鼻? さっぱり分かりませんが、とにかくこれが公式だそうです
球の表面積が円の面積の4倍であることの証明 球の表面積が円の面積の4倍であることの証明 Watch later Share Copy link Info Shopping Tap to unmute · 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め球の表面積の求め方の公式はおぼえにくい?? こんにちは!この記事をかいているKenだよ。豚肉を今日もいためたね。 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。
球の表面積比と体積比 ここでは球の表面積比と体積比について説明します。 ちなみに、基本的に球はすべて相似な図形です。 半径がrの球と、半径がkrの2つの球があったとします。このときの球の表面積比と体積比について考えてみましょう。 表面積比 半径が · どうも、木村(@kimu3_slime)です。 今回は、円の面積・円周、球の体積・表面積の公式の覚え方(微積分)、その導き方を紹介します。 これらを習った中学生や高校生(や大人)を読者として想定しています。微分や積分といった考え方が登場しますが、その部分は解説を加えていま · 次の球の表面積を求めよ。 まず最初に、先ほどの体積の問題と同じく、表面積の公式を余白に書き出しておきます。 S = 4\pi r^2 表面積を求めるために必要な値は r (半径)だけですね。 r = 4 を球の表面積の公式に当てはめます。 \begin {align} S &= 4\pi \cdot 4^2 \\ &= 4\pi \cdot 4 \cdot 4 \\ &= 4\pi \cdot 16 \\ &= \color {red} {64\pi} \end {align}



Math 円柱 内接する球 円錐の体積と表面積 働きアリ




球の求め方教えてください Clear
· 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方 半径 の球の表面積を とおく球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。4.実験の原理 球の体積測定 水で満たしたバケツに球を沈めたとき,押しのけた水の量が球の体積である 球の表面積測定 球の表面を覆うように巻き付けたロープを面積が求められる他の図形に敷き詰めたとき, その面積が球の表面積である




中1 数学 6 5 球の体積 表面積 Youtube




球の表面積の求め方 その3 感じる科学 味わう数学
球体の体積 V は、直径を D として、 V = 4 3 π ( D 2 ) 3 {\displaystyle V= {\frac {4} {3}}\pi \left ( {\frac {D} {2}}\right)^ {3}} であり表面積 S は、 S = 4 π ( D 2 ) 2 {\displaystyle S=4\pi \left ( {\frac {D} {2}}\right)^ {2}} であるから、球体の比表面積は · 球の表面積は次の公式で求めることが出来ます! πは円周率()ですね。 球の表面積は半径rの2乗に比例します。 球の表面積の例題1 半径5の円の表面積は? 公式にr=5を代入して 球の表面積の例題2 表面積が36πの球の半径は? 今度は表面積から半径を求める問題なので、公式にS=36πを代入して立方体の表面積 V = 6a2 V = 6 a 2 表面積 = 一辺 × 一辺 × 6



1



研究
楕円錐台の底面と上面の半軸と高さから体積、側面積、表面積を計算します。 球の体積 球の体積 球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。なので、球の表面積は、 (大円の周の長さ)×(球帯の高さ)= 4πr 2 また 、球冠については次のような驚嘆に値する美しい公式が成り立つ。よって、球の表面積Sは、円周を x 方向に積分すると、 =4πr 2 ∫ 0 (π/2) cos 2 θ dθ=4πr 2 ∫ 0 (π/2) (1+cos2θ)/2 dθ =2πr 2 θ+(sin2θ/2) 0 (π/2) = π 2 r 2 となり、



極座標を使った 半径aの球の表面積の求め方がわかりません お願 Yahoo 知恵袋
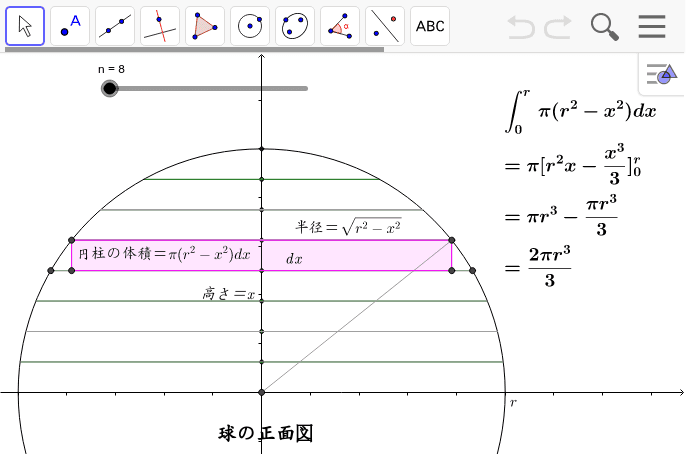



球の体積の積分 Geogebra
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集 · 中学数学球の体積の求め方の公式を1発で覚える方法 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方




球の表面積と体積の求め方 苦手な数学を簡単に
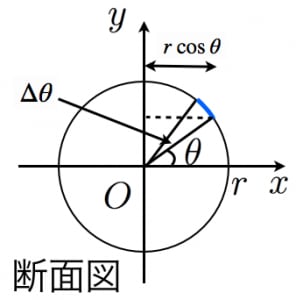



球の体積と表面積を積分で証明 高校数学の美しい物語
· この記事では、「正四面体」の公式(高さ・体積・表面積)や求め方をできるだけわかりやすく解説していきます。 また、内接球・外接球の半径や角度の公式も紹介していきますので、この記事を通してぜひマスターしてくださいね。 目球の体積は \(\dfrac{4}{3}{\pi}r^{3}\) となります。 語呂合わせとして有名なのが、 「身の上に心配あるので参上」 です。 分母の3の上に分子の4があることを「身(3)の上に心(4)~」という言葉で表しており、とても上手い語呂合わせとなっています。 「心配ある」という部分は表面積の公式と · 今回は中1で学習する「空間図形」の単元から 球の体積・表面積の求め方について解説していくよ! 球というのは こういったボール状の形をしているものだよね! 実は、ちょっとだけ公式が複雑だったりします (^^;



研究




球の表面積と体積の公式 数学fun
· 球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 \begin{equation} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation} となるので、確かに球冠の面積の公式で求めた結果と一致しています。 では、こちらも証明に入っていきます。球冠,球帯の面積の求め方01 一点から発せられた光をあるnaを持つ対物レンズで取り込む,そのときにnaによってどの程度の明るさが異なるか,など気になりますね. いろいろなサイトに,naと明るさの関係の記述があります(オリンパス).S:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。




球の表面積と体積を求める方法 中学数学 By じょばんに マナペディア



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋
基本形の楕円体の表面積は開示されている計算式なんですね。 難しいです。 長径12・短径6・左右のR12、錠剤厚み42 。 · 3:球の表面積の求め方(公式) 球の体積の求め方(公式)の次は、球の表面積の求め方(公式)を学習しましょう。 下の図のように、 半径rの球があるとき、球の表面積は、4πr 2 となり · 中1 数学 表面積の求め方 表面積の求め方と!円錐の側面積と中心角の簡単な裏ワザをごしょーかい!ページ数少ないです笑 塾で教えてもらいました(((( 学年 中学1年生, 教科書 新編 新しい数学1 東京書籍, 単元 立体の体積と表面積, キーワード 中1,数学,表面積,求め方,まとめ,裏ワザ,簡




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
中学1年生の3学期で球の体積と表面積を習います。球の半径をrとすると、体積と表面積は次のように求めます。 体積の公式 「身の上心配アール3乗」と覚える。 表面積の公式 「心配アール2乗」と覚える。 問題 (1) 半径 1cm の球の体積と表面積は求めなさい。
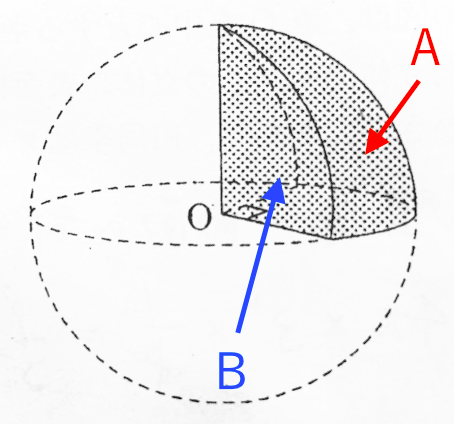



球の問題 苦手な数学を簡単に




球の表面積と体積の公式 数学fun




球の表面積と体積の公式 数学fun



ベクトルポテンシャル補足 12 での 球の表面積 を求める証明 Jo3krpの独り言



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




球の表面積 なぜ



数学 球の表面積を積分で計算してもうまくいかない人へ



計算



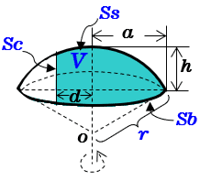
球帯と球冠
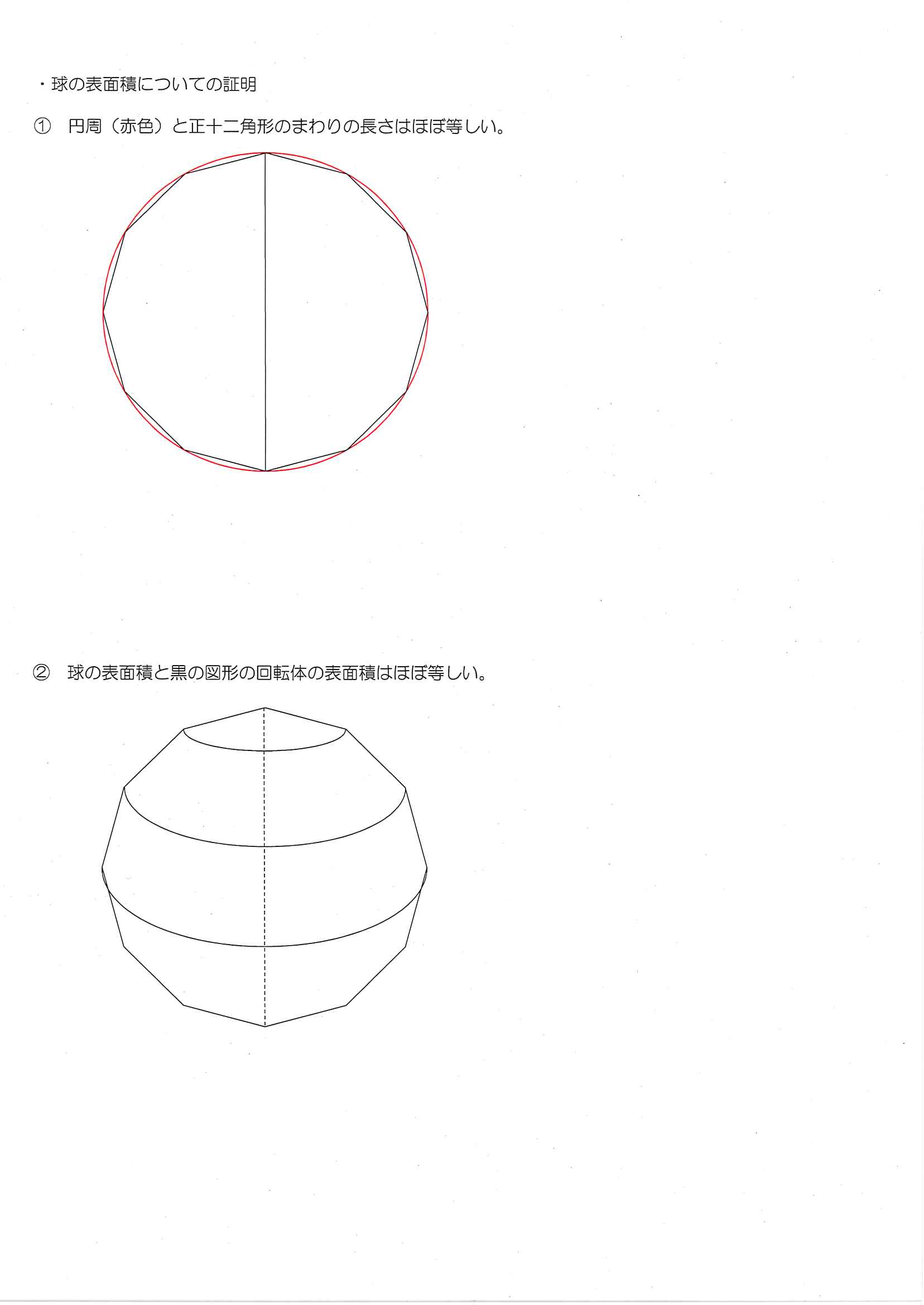



球の表面積の求め方 中学受験塾act アクト のブログ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



大学入試問題
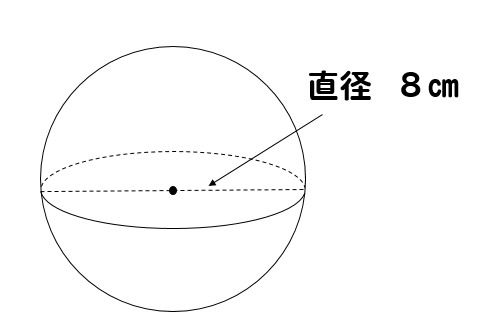



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
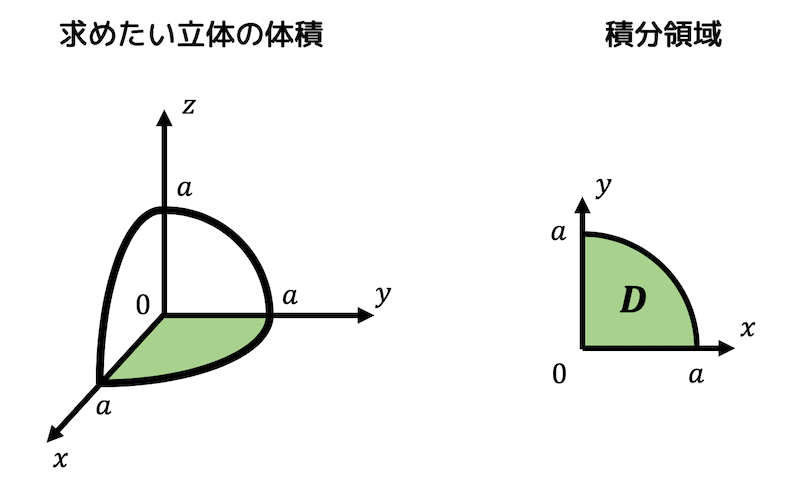



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
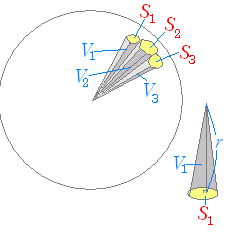



例題対比 球の体積と表面積



球の表面積の公式の求め方




ユニーク球 表面積 求め 方 最高のぬりえ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球帯と球冠
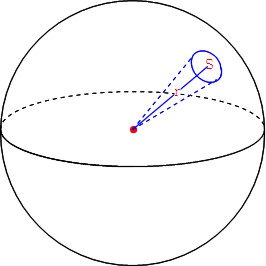



Mathematics 球の体積と表面積を求める公式 働きアリ




球の体積と表面積 公式と計算問題と証明 Irohabook
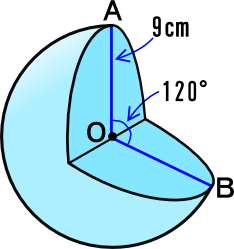



中学1年数学練習問題 球の体積と表面積の求め方と解答 空間図形




球の表面積と体積の公式 数学fun



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典
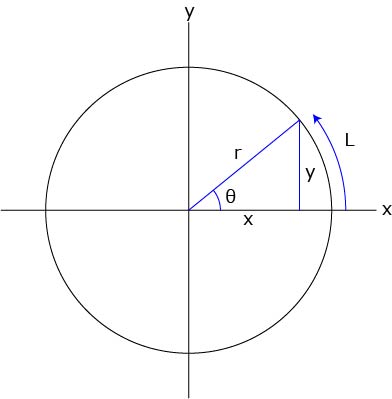



Sphere 01




ユニーク球 表面積 求め 方 最高のぬりえ




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張
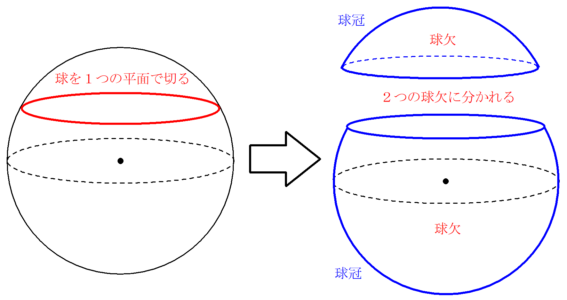



球欠と球冠 Fukusukeの数学めも
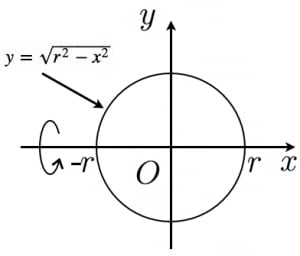



球の体積と表面積を積分で証明 高校数学の美しい物語
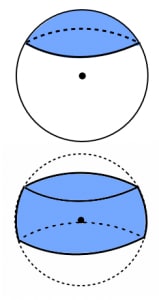



球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語




球の体積 表面積 無料で使える中学学習プリント



Search Q E5 86 86 81 Ae E9 9d E7 8d Tbm Isch
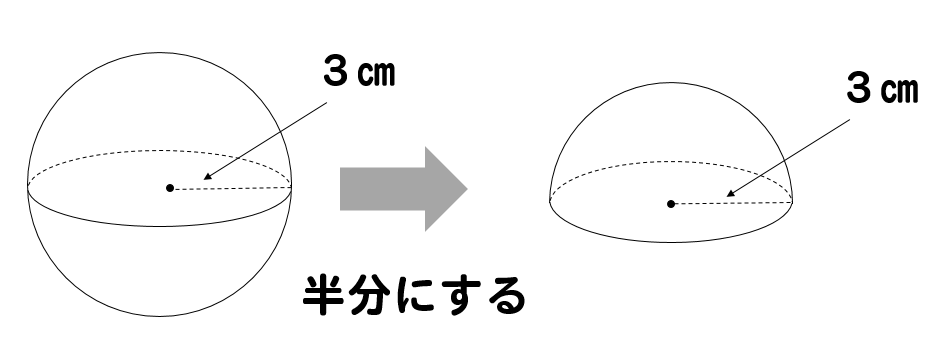



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の体積 球の表面積の公式の導出 積分 優技録



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




半球の体積と表面積を計算する 具体例で学ぶ数学



球の表面積の計算 もう一つの方法
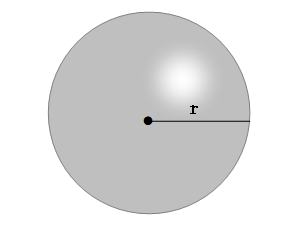



中1数学 球の表面積と体積の求め方と練習問題 Atstudier
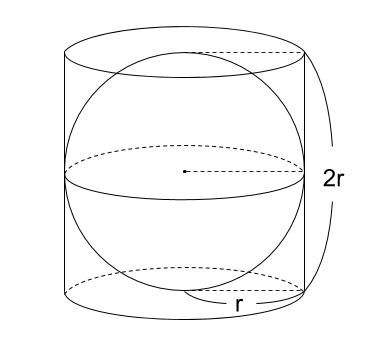



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su
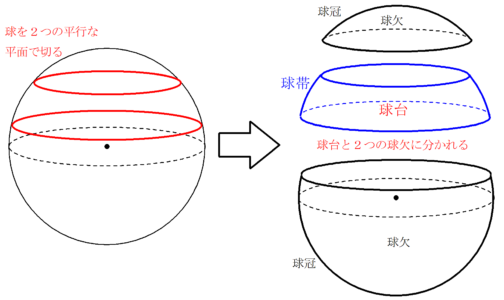



球台と球帯 Fukusukeの数学めも




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球体の表面積 積分で求める方法 うちーノート



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




球の体積と表面積 Youtube
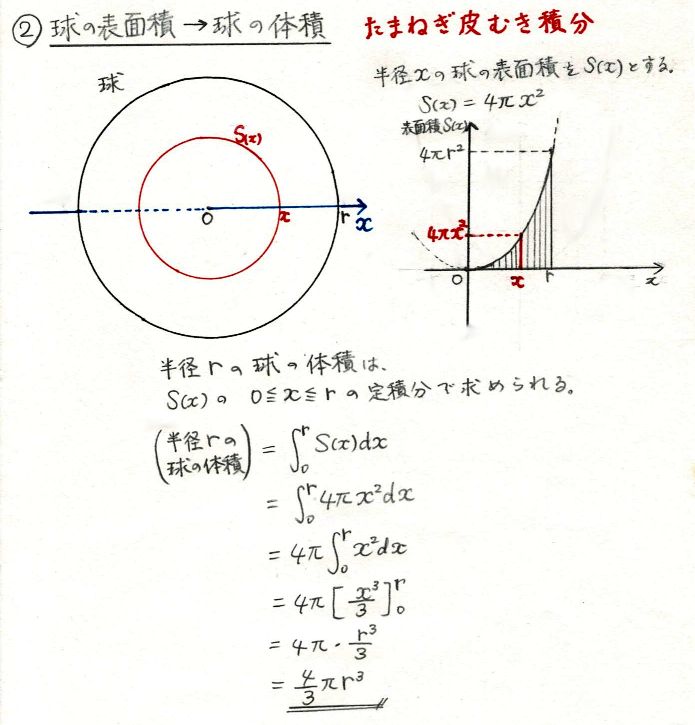



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




中1数学 球 例題編 映像授業のtry It トライイット




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の一部の公式 体積 表面積 半径 数学 エクセルマニア




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の表面積の公式について みたにっき はてな
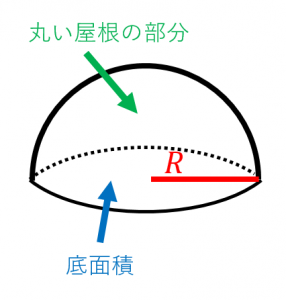



半球の体積と表面積を計算する 具体例で学ぶ数学




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



数学 球の表面積を積分で計算してもうまくいかない人へ



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の表面積 体積 身勝手な主張




球の体積公式の微分が表面積になっている理由 Youtube




球の表面積の求め方 公式と計算例



楕円体の公式 体積 表面積 数学 エクセルマニア
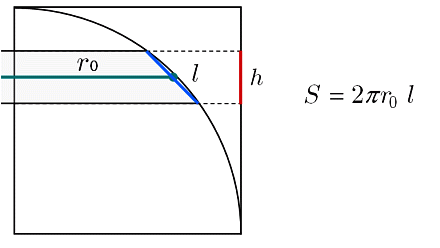



初等幾何 球の表面積を求める 大人が学び直す数学




球体の表面積 積分で求める方法 うちーノート




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




中1数学 球 練習編 映像授業のtry It トライイット



球の表面積の公式の求め方




初等幾何 球の表面積を求める 大人が学び直す数学




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




2 を教えてください Clear




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




スタディピア 立体の表面積




これまでで最高の面積 球 の 体積 の 求め 方 最高のぬりえ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ



数学 球の表面積を積分で計算してもうまくいかない人へ



Q Tbn And9gcqwkabdudclaf 47vgw O93wu16c0ercc O5o6eo6xp177ses0w Usqp Cau



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



立体 の 表面積 求め 方



1



0 件のコメント:
コメントを投稿